Introduction
The primary advantage of confocal microscope imaging over traditional widefield fluorescence microscopy is the rejection of light from regions positioned away from the focal plane, leading to the ability to obtain thin optical sections with increased contrast that can be assembled into interpretable three-dimensional image stacks. Because optical sectioning is a prerequisite for a number of applications, including precise localization studies, co-localization experiments, and spectral unmixing, a large variety of different optical sectioning techniques have been developed and commercialized over the past few years. The laser scanning confocal microscope (LSCM) remains the gold standard for many applications, but single point scanning is severely limited in acquisition speed. Due to the fact that the image is assembled point-by-point (one pixel at a time), attempting to employ high frame rates will ultimately lead to very short pixel dwell times and, therefore, often insufficient signal-to-noise ratio (SNR) in the final images or optical sections. Alternative microscope designs attempt to overcome this unfortunate speed limitation by scanning multiple points in parallel, which can increase acquisition speed dramatically, but at the cost of spatial or axial resolution. It should be noted, however, that all of these instruments are based on laser illumination, which restricts their spectral flexibility and results in high system prices.

Microscope systems that do not rely on laser illumination but instead use a simple white light source, such as arc-discharge lamps or LEDs, present an attractive alternative to laser-based instruments for optical sectioning as they offer dramatically enhanced spectral flexibility for a relatively low price. The concept of structured illumination microscopy (SIM), which can be implemented on a standard widefield fluorescence microscope, offers such an option. In structured illumination systems, the excitation light is patterned in a defined geometrical pattern, and this additional information is used to mathematically extract an optical section from a series of raw data images. SIM systems all follow the same technical principle that consists of an illumination mask to structure the excitation light with a specific (usually based on a line grid) pattern. As the illumination mask is located in a conjugate image plane, the pattern will only appear in focus at the focal plane of the instrument. At positions residing away from the focal plane, the pattern will be blurred. Thus, the patterned structured illumination will generate fluorescence emission from the focal plane that is modulated in accordance to the grid pattern, whereas emission from other planes will not be modulated.
The key to calculation of an optical section image when using structured illumination is demodulation of the raw data image set. The software algorithm must identify the modulated part of the signal representing the in-focus information and separate that from the unmodulated signal arising from other focal planes. Image processing of SIM data is usually conducted post-acquisition by demodulating the image set (usually three or more images), which consists of images having the illumination pattern in different positions. Changes in pixel intensities in between the three or more images can be attributed to the different pattern positions, representing the modulated response from in-focus structures, while intensities that are not influenced by the position of the illumination pattern represent out-of-focus information. Such systems, as realized in the ZEISS ApoTome, have matured over the last years into viable low-cost alternatives for optical sectioning. However, the acquisition speed of such a system remains limited by the necessity to acquire several images in order to calculate one optical section.
back to top ^Concept of Aperture Correlation Microscopy
Aperture correlation microscopy combines the light efficiency of structured illumination with the acquisition speed of a spinning disk confocal instrument. The technique promises to push SIM into new applications where high temporal resolution is mission-critical, while simultaneously maintaining the relatively simple instrumentation (especially the use of a white light source) of other SIM instruments. A necessary step for increasing the speed of SIM image acquisition involves abandoning offline demodulation techniques. Instead, demodulation must be conducted not only by illuminating the sample through a structured mask, but also by employing the same mask for detection in order to directly identify emission from the focal plane. The goal of aperture correlation microscopy is to overcome the limited light efficiency of traditional spinning disk systems where a multi-pinhole array is used to sweep across the specimen and probe the sample at several points in parallel. Incorporating a spinning disk into confocal microscopy dramatically speeds up image acquisition, but in order to maintain resolution and confocality, the pinholes must be placed far enough apart to prevent out-of-focus light from reaching the detector through neighboring pinholes (a phenomenon referred to as pinhole crosstalk). Thus, only a few percent of the excitation light will actually pass through the pinhole array, most of it being blocked at the regions in between the pinholes, which makes laser illumination almost mandatory in these systems.
The principle concept behind aperture correlation is to overcome the pinhole crosstalk limitation by using temporal rather than spatial coding. In effect, instead of probing each pixel only once with a spatially uniquely positioned pinhole, the idea is to probe each pixel multiple times but with a temporally unique sequence. Each pixel is presented with a sequence of pinhole illuminations that shows zero cross correlation to the sequence presented to any other pixel. Thus, for each pixel in the image, a temporal modulation of an aperture transmission according to an appropriate correlation sequence must be found (thus the name aperture correlation). The temporal coding necessary for aperture correlation can be achieved by a dense, random pattern of pinholes on a rotating disk. In this manner, each pixel will be probed several times through different pinholes, but for each pixel the illumination sequence will be random, and thus unique. A major limitation is that such an instrument cannot directly provide a confocal image as this would require negative transmission values for the blocking areas of the disk. In reality, the image detected through the disk contains all the in-focus information plus an offset representing out-of-focus information.
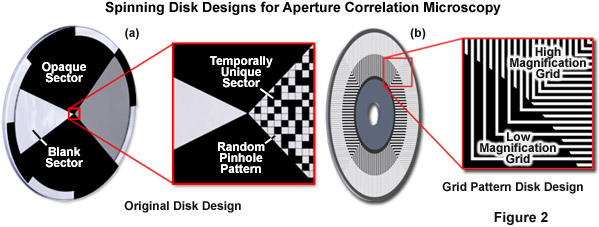
In order to calculate an optical section, the out-of-focus offset must be subtracted. Toward this end, the original design (see Figure 2(a)) included a blank sector on the disk through which a standard widefield image could be acquired. Scaled subtraction of both images resulted in an optical section. The primary advantage of this design is that the random pinhole pattern used for illumination and detection can be very closely packed. Therefore, up to 50 percent transmission efficiency can be achieved, which allows use of a standard white light source. In summary, the idea of aperture correlation allows for a very light-efficient disk design so that a normal white light source is sufficient and no laser illumination is required. However, in order to achieve this, the condition of directly acquiring an optical section must be relaxed, and the optical section has to be calculated by a scaled subtraction from two raw data images.
Presented in Figure 2 is the original disk design for aperture correlation microscopy (Figure 2(a)) along with the more advanced design using a grid line pattern (Figure 2(b)). In the original design, a random pinhole pattern is used that can only be optimized for one objective. In the more advanced grid pattern design, two different grid patterns are located on the same disk to eliminate the requirement for changing disks to match objective numerical aperture. In short, the magnification and numerical aperture of the objective combined with the spatial frequency of the grid pattern on the disk define optical section thickness. The high and low magnification patterns illustrated in Figure 2(b) are designed to be compatible with a wide range of objectives, which are outlined in Table 1.
back to top ^Optical Layout and Imaging Process
As discussed above, the first generation aperture correlation instrument design required sequential acquisition of two images: the image detected through the random pinhole pattern containing the in-focus information overlaid by a widefield offset and a standard widefield image through a blank section on the disk. This design required tight synchronization of the disk rotation with camera exposure. More importantly, such sequential image acquisition will lead to problems when imaging dynamic processes. Any movement that occurs between capture of the two images will result in motion artifacts in the calculated optical section. In order to prevent this, both images that are necessary for calculation of the optical section must be acquired simultaneously. Such a requirement was rendered possible by a new design (Figure 2(b)), which uses both the light detected through the disk as well as the light being blocked at the disk to capture both the conjugate image (the image detected through the disk containing in-focus information and the out-of-focus offset) and the non-conjugate image (containing only out-of-focus information) simultaneously.
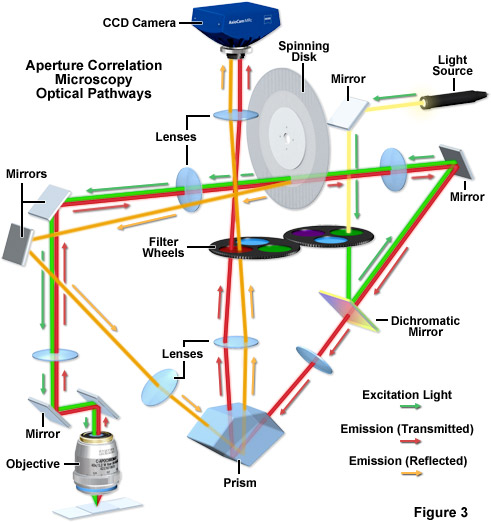
The principal lay-out of the ZEISS VivaTome, a commercially available aperture correlation spinning disk system, is presented in Figure 3. A rotating disk having a defined grating pattern is located in one of the microscope conjugate image planes. Excitation light is directed through this disk, and the transparent regions on the disk are placed very close together so that approximately 50-percent transmission efficiency through the disk is achieved. As a result, any normal white light source (such as a metal halide lamp) will provide sufficient excitation intensity. Emission from the sample is again directed to the disk through the optical train, and the emission light from the focal plane will be focused through the openings on the disk and subsequently onto the detector. However, because to the disk layout features densely packed openings, out-of-focus light will also randomly pass through the disk (see above). With a 1:1 line-to-space ratio (50 percent of the disk being transmissive), 50 percent of the out-of-focus light will make it through random openings in the disk. Thus, the image detected through the disk contains all the in-focus information but also 50 percent of the out-of-focus information. In order to capture the additional information needed to calculate an optical section disk positioning geometry is critical. The disk is positioned at a slight angle to the optical pathway, and the side facing the specimen is reflective. This architecture enables the out-of-focus light normally blocked at the disk to be reflected into a second imaging beam path that is finally imaged onto the camera side-by-side with the image detected through the disk. In the second image, the other 50 percent of the out-of-focus light is captured. Using the side-by-side detection strategy for both images, all the information needed to calculate the optical section is captured simultaneously on one camera and motion artifacts can be excluded.
In aperture correlation microscopy, the final image is calculated in three steps: first, the two images have to be extracted from the side-by-side view and one image is mirrored to match the image orientations. The second step involves a registration of both images to ensure that the overlay is precise on a pixel-by-pixel basis. In the registration step, distortions as mapped in a previous calibration step are corrected between the two imaging beam paths. The third step is the actual calculation of the optical section itself. A scaled subtraction of both images will yield the optical section. Conversely, a scaled addition of both intensities results in a normal widefield image, as all intensities from the sample are then combined in one image. The scaling factor (k) is used to correct for small differences in transmission efficiencies in the two imaging beam paths:
IOptical Section = ITransmitted - k • IReflected (1)
IWidefield = ITransmitted + k • IReflected (2)
In equations (1) and (2), the term on the left-hand side (IOptical Section or IWidefield) denotes the pixel intensity in the final image, whereas the ITransmitted and IReflected terms represent the pixel intensity in the image resulting from light transmitted through the disk or reflected from the surface of the disk, respectively. As discussed, the term k is a scaling factor designed to correct for transmission differences in the separate optical pathways of the transmitted and reflected light. It is noteworthy that although the final image is calculated, the entire calculation is strictly linear in respect to pixel intensity and, therefore, the intensity in the final section image can be directly correlated to the original intensity. As a result using aperture correlation microscopy images for quantitative intensity analysis is straightforward.
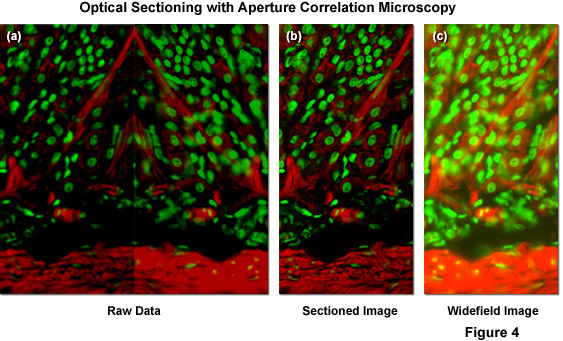
Illustrated in Figure 4(a) is typical raw image data generated by a ZEISS VivaTome aperture correlation microscope, as well as images representing the calculation of an optical section using equation (1) and (2) above. The specimen is a thick (16 micrometers) cryosection of rat stomach (fundus region) stained with Alexa Fluor 568 conjugated to phalloidin to highlight filamentous actin and counterstained with SYTOX Green to label nuclei. Within the raw image data, both the fluorescence detected passing through the disk (containing a conjugate image containing both widefield plus in-focus information; right side of Figure 4(a)), and fluorescence rejected at the disk (a non-conjugate image containing widefield data minus the in-focus information; left side of Figure 4(a)) are contained. During post-acquisition image processing both images are extracted, one half is mirrored, and both images are registered to account for differences in the imaging paths. A scaled subtraction results in an optically sectioned image (Figure 4(b)), whereas a scaled addition results in a conventional widefield image (Figure 4(c)). Thus, a scaled subtraction of the two image halves results in one image containing only the confocal information and a scaled addition of both image halves adds all the intensity from the specimen to produce a normal widefield image.
back to top ^Resolution, Sectioning Strengths, and Depth Penetration
The structure on the spinning disk ultimately determines the axial resolution of an aperture correlation instrument, and a number of different approaches to disk design have been published. The original design used pinhole-like structures that resulted in images formally equivalent to those obtained with a confocal microscope. An attractive alternative is the use of a simple grid line pattern. With such a design, the optical section thickness is dependent on the numerical aperture and the magnification of the objective and the frequency of the grid. To a first approximation, the axial response of the instrument can be described by equations (3) and (4):
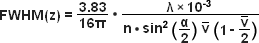 (3)
(3)
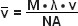 (4)
(4)
In equations (3) and (4), λ refers to the wavelength in nanometers, n is the refractive index of the immersion medium, α is the aperture angle of the objective (numerical aperture; NA = n • sinα), 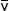 is the effective grid frequency in the specimen plane with an objective having a magnification of M, and ν is the actual grid frequency.
is the effective grid frequency in the specimen plane with an objective having a magnification of M, and ν is the actual grid frequency.
In typical slit scanning spinning disk microscopy systems, axial resolution is sacrificed in order to increase light throughput efficiency. In effect, for the efficient use of a white light source, the individual slits must be placed relatively closely together, which in turn decreases the sectioning ability of the instrument. The strength of aperture correlation microscopy is that it offers the highest light efficiency without having to suffer a compromise in axial resolution. By taking two images and calculating the optical section from the additional information, both the highest light throughput efficiency and excellent sectioning can be obtained. In theory, such a design can achieve remarkable axial resolution, even outperforming a traditional point scanning confocal. However, at high axial resolution, the performance of an aperture correlation instrument (like any other optical sectioning system) becomes ultimately limited by signal-to-noise. As a result (especially when imaging biological specimens), the true sectioning performance of an aperture correlation instrument can seldom be realized, as most biological samples are clearly limited in their available signal. In these cases, it is therefore a better option is a compromise offering good axial resolution (comparable to the resolution on a point scanning confocal with the pinhole set to 1 Airy unit), but still providing sufficient signal-to-noise in the final image (even for normally weakly fluorescent biological samples). In order to match the specifications of various objectives, different grid frequencies must be available to achieve optimal sectioning. As an example, the ZEISS VivaTome offers two grid patterns that cover the full range of magnifications (see Table 1; + indicates the best compromise for a given objective).
Objective Specifications for Aperture Correlation Microscopy
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 1
The lateral (x,y) resolution of a structured illumination instrument using a grid pattern (including aperture correlation microscopes) is comparable to that of any widefield fluorescence microscope. In effect, resolution is essentially diffraction limited. Furthermore, if the disk design takes into account the need for different grid orientations during image capture, the lateral resolution of an aperture correlation system remains isotropic. Another advantage of using a grid pattern on the disk is the reduced need for synchronization with the detector system. In spinning disk microscope systems, during a given exposure time, all pixels in the image must be illuminated the same number of times so that the entire image appears evenly illuminated. In the case where pinholes or slits are sparsely positioned (as found in traditional spinning disk instruments) this requires either a tight synchronization of disk rotation to camera exposure or exact matching of disk rotation speed to camera exposure time. In contrast to an array of pinholes, with a grid pattern minimal rotation of the disk will ensure complete illumination of the field of view because only one line pair of the grid is needed. Given a reasonable disk speed of approximately 3000 revolutions per minute, the image will be averaged over so many line pairs within a normal exposure time used in live cell imaging (tens of milliseconds) that an even field of illumination is ensured without the need of tight synchronization.
The penetration depth of any structured illumination system is ultimately limited by two factors: the dynamic range of the camera and modulation contrast (in effect, the contrast transfer function). As the optical section is calculated from a raw data image containing both the in-focus and the out-of-focus information, the in-focus intensity captured in the raw data image must be sufficient for a sectioned image of good quality even against strong out-of-focus background (see discussion below). This means the camera must have sufficient dynamic range to compensate for higher light levels. However, increasing the dynamic range of the camera will only help to a certain point. If the out-of-focus fluorescence emission is overwhelming, the modulation of the excitation intensity by the grid is no longer detectable. Loss of grid modulation due to an unfavorable signal-to-background ratio is the factor that ultimately limits the depth penetration of any structured illumination.
back to top ^Detectors for Aperture Correlation Microscopy
The primary considerations in imaging living or fixed cells and tissues in the microscope with a digital camera are detector sensitivity (signal-to-noise), the required speed of image acquisition, and specimen viability (for live cells). The relatively high light intensities and long exposure times that are typically employed in recording images of fixed cells and tissues (where photobleaching is the major consideration) must be strictly avoided when working with living cells, where phototoxicity considerations prevail. In virtually all cases, live-cell microscopy represents a compromise between achieving the best possible image quality and preserving the health of the cells. Rather than unnecessarily oversampling time points and exposing the cells to excessive levels of illumination, the spatial and temporal resolutions set by the experiment should be limited to match the goals of the investigation.
Aperture correlation systems, such as the ZEISS VivaTome, can be used with virtually any scientific grade CCD or low light level electron-multiplying (EMCCD) camera, but the technique poses several demands on the detector that must be considered. First of all, due to the requisite side-by-side capture of two images on a single chip, using only half the chip must still offer a reasonable field of view. Furthermore, the number of pixels and the pixel size on the chip should be sufficient to provide the required resolution when considering that the final image will be only half the original chip size. In most cases, but especially when dealing with weakly fluorescent biological samples, high sensitivity is mission-critical when choosing a camera. With all structured illumination microscopy systems, the dynamic range of the camera system also becomes very important when attempting to image thicker (usually tissue) specimens, because the primary task of detectors in such systems is to gather the scant in-focus information as efficiently as possible. Due to the fact that in most optical sectioning techniques (such as traditional spinning disk systems), out-of-focus light is physically blocked (by the pinholes or slits) from reaching the detector, the cameras designed for use in these systems must be optimized for highest sensitivity.
In structured illumination microscopy systems, all the fluorescence emission emitted by the sample (with the exception of that lost in the optical train) impacts the detector with the in-focus information subsequently being extracted mathematically. Therefore, in addition to the requirement for being highly sensitive, the detector of a SIM system must be able to precisely deal with a broad spectrum of intensities rather than just low light levels, and therefore, a high dynamic range is necessary. The level of dynamic range needed varies from specimen to specimen and is primarily determined by the ratio between in-focus and out-of-focus intensity in the raw data images. If a SIM system is used on a relatively thin specimen, the demand on the dynamic range requirements of the camera is moderate, as the in-focus information accounts for a significant part of the total intensity in the raw data image. However, if a SIM system is used on a thicker, highly fluorescent specimen, the out-of-focus information will dominate. Thus, in order to have sufficient dynamic range in the calculated sectioned image, enough in-focus information must be included in the raw data image against the strong out-of-focus background. In such a situation the camera dynamic range can be the limiting factor in overall performance of the instrument.
Dynamic range is defined by the full-well capacity of the photodiodes divided by the readout noise of the camera. As an example, if the full-well capacity is approximately 17000 electrons and the readout noise is around 7 electrons, the dynamic range of the camera is close to 1:2400. In effect, the camera is able to distinguish 2400 different light levels. There are two mechanisms available to increase the dynamic range of a camera that involve either increasing the full-well capacity of the photodiodes or reducing the readout noise. The full-well capacity is essentially a fixed feature of pixel size and dimensions in the original chip design and is therefore not easy to change. The readout noise, on the other hand, can be influenced by reducing the readout speed. By reading the chip data at a slower rate, the readout noise can be dramatically reduced, resulting in a higher effective total dynamic range. However, reducing readout speeds also result in a commitment reduction in frame rate because the total readout time is increased.
Another factor influencing the dynamic range of a camera is any amplification step carried out before the conversion of analog voltage values to a digital format (analog-to-digital conversion; A/D). This is an important factor when an EMCCD camera is to be used in combination with a SIM system. The electron-multiplying gain on an EMCCD camera leads to a tremendous amplification of the original signal that enables EMCCD cameras to reliably detect single photons above the noise floor. However, the photodiode wells of the multiplication register have a limited full-well capacity. Because the detector in a structured illumination microscope will always be exposed to virtually all the light emitted by the specimen, amplification will start not with a single photoelectron, but with a significant number of photoelectrons. Amplification of the signal can easily reach saturation in the multiplication register.
In summary, the choice of the detector for any SIM system is always a compromise between the frame rate, sensitivity, and dynamic range. In cases where predominantly thicker samples are imaged, the higher dynamic range of a scientific grade CCD camera may be more important. However, if the system is to be optimized for thinner samples (such as live cells), the limited dynamic range of an EMCCD camera may still be sufficient, allowing for higher sensitivity and most importantly, higher frame rates.
back to top ^Conclusions
Aperture correlation microscopy is an attractive technical approach to fast optical sectioning with relatively simple instrumentation. The technique offers artifact-free images, even when observing highly dynamic processes at high frame rates, and is usually only limited by the available signal and necessary exposure time. Use of a white light source ensures spectral flexibility at a low price. Furthermore, this methodology offers excellent sectioning performance without compromising axial or lateral resolution. Performance is ultimately limited by signal-to-noise, and on many specimens it will result in images comparable to any other optical sectioning technique. Aperture correlation is well suited for thin to medium specimens, however, in thick or highly scattering specimens it is limited (as are other SIM techniques) by signal to background. For optimal performance, a detector with a good compromise between sensitivity, dynamic range and frame rate is necessary. In summary, aperture correlation offers high speed and high quality optical sectioning using simple and affordable instrumentation.
Contributing Authors
Matthias F. Langhorst - Carl Zeiss MicroImaging GmbH, Koenigsallee 9-21, 37081 Goettingen, Germany.
Rimas Juskaitis - Aurox Limited, Culham Science Centre, Abingdon OX14 3DB, United Kingdom.
Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.







